1 引言
金宝搏app由于无压力损失、成本相对较低等优点,其应用越趋广泛,同时也要求金宝搏app朝着更加稳定、精度更高、重复性更好和使用寿命更长的方向发展。因此,如何提高金宝搏app的测量精度这一课题具有非常重要的研究意义。
2 金宝搏app基本原理
金宝搏app是一种测量导电液体流量的仪表,传感器部分主要由线圈,测量电极,钢管和绝缘内衬组成,如图1所示。其工作原理是:由电源驱动线圈,在管道内形成稳定磁场,电极、电极导线及两电极间的液体组成封闭回路,当导电液体流过时,切割磁力线,在电极两端产生感应电动势。
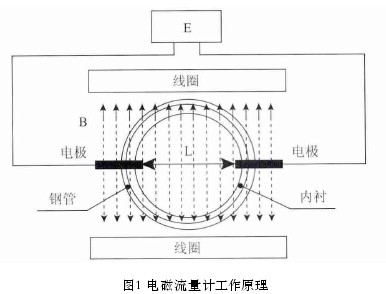
假设磁场B均匀,根据法拉第原理:
E=B×L×V
目前,金宝搏app的设计均基于这一理论基础。
3 金宝搏app仪表系数
当一台金宝搏app完成装配后,在同一工作环境或温度下,其线圈参数是相对固定的,因此,电流稳定后,磁场强度B是固定的,而两电极间的距离L也是恒定的,因此感应电动势E值与导电液体的流速V成正比。
变送器收集电极的电压信号,进行放大,滤波降噪,以脉冲频率或其它方式输出流量信息。本文以脉冲频率输出为例,其脉冲频率与电极间的感应电动势成正比关系,即脉冲频率与感应电动势一一对应,目的是建立数据传输过程中信号值的唯一性,因此有:
P=μ×E
上式中,P为输出脉冲频率,μ为正比系数,因此有:
P=μ×B×L×V
即输出脉冲频率P与介质流速V成正比,令K=μ×B×L,则有:
P=K×V
在金宝搏app行业,定义K为增益,它是金宝搏app仪表系数的重要组成部分。一台理想的金宝搏app,输出脉冲频率与介质流速之间的关系如图2所示。
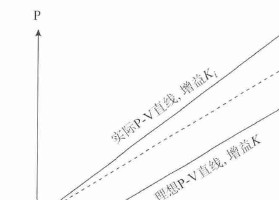
然而,在实际的生产过程中,由于受生产工艺稳定性的影响,会累积各种误差,累积误差在输出脉冲频率与介质流速间的关系中,分为增益误差与零点偏置误差,增益误差表现为每台金宝搏app的增益Ki(i=1,2,3,...)值是不同的,而偏置误差表现为零点漂移,即在零流速下,输出脉冲频率不为零,因此:
P=Ki×V+bi
另外,每台流量计的增益Ki及零点偏置值bi均不一样,由增益与零点偏置组成每台金宝搏app的仪表系数。
由于受生产效率的限制,基于以上理论,金宝搏app的标定普遍采用两流速点标定,然后拟合成直线,从而计算出增益与零点偏置值。但是两点拟合具有局限性,在不同流速下,两点拟合获得的仪表系数是否线性,以及线性度如何,目前还没有相关的论文进行叙述或分析,因此通过标定试验分析,研究金宝搏app实际仪表系数的线性度,及其对精度的影响,具有非常重要的意义。
4 实验步骤
选择DN50的表进行标定实验,整个实验过程中只采用一次安装,实验的具体步骤如下:
第一步:通过0.3m/s与3.0m/s两流速点标定,获得两点标定的仪表系数K1,并在0.3m/s,0.9m/s,1.8m/s,3.0m/s,4.6m/s的流速下验证仪表系数,每个流速验证5次;
第二步:从第一步的验证数据中,选择不同的流速点拟合计算标定系数;
(1)5个流速点进行拟合,获得仪表系数K2;
(2)0.3m/s与0.9m/s两个流速点进行拟合,获得仪表系数K3;
(3)1.8m/s与3.0m/s两个流速点进行拟合,获得仪表系数K4;
第三步:在5个流速下验证仪表系数K2,K3,K4,每个流速各自验证5次。
5 实验结果
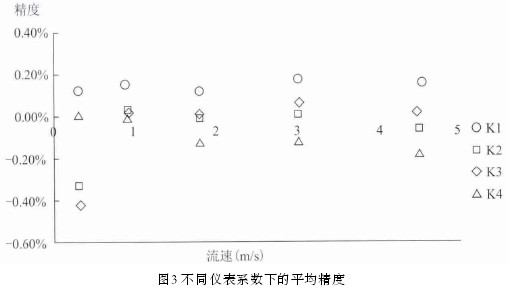
如表1所示为不同流速点拟合获得的仪表系数,各个仪表系数下验证的平均精度如图3所示。

6 分析
(1)不同仪表系数在不同流速下的精度有差异,在某特定流速点,精度受拟合点的影响;
(2)由0.3m/s与0.9m/s两流速点拟合获得的仪表系数,系数验证时,在0.3m/s与0.9m/s两个流速下获得的平均精度要比其他系数的高;
(3)由5个流速点拟合获得的仪表系数,系数验证时,在0.9m/s,1.8m/s,3.0m/s和4.6m/s流速下获得的精度高:
(4)由1.8m/s与3.0m/s两流速点拟合获得的仪表系数,系数验证时,其精度与5个流速点拟合获得的仪表系数相当;
(5)相对与其他仪表系数,由0.3m/s与0.9m/s两流速点拟合获得的仪表系数与5个流速点拟合获得的仪表系数相差较大,即低流速范围内的仪表系数线性度要比高流速范围内的线性度差。
7 结论
金宝搏app的实际标定系数并非绝对线性,而是在一定误差范围内可以认为是线性的;金宝搏app标定系数的线性度是金宝搏app的测量精度的重要影响因素;
在生产工艺一定的情况下,标定系数的算法对测量精度也有很大的影响,因此,实际生产中应根据金宝搏app的精度等级,适当调整标定工艺及标定系数的算法;
金宝搏app的线性度应该作为一个重要的性能指标进行量化;进一步研究影响仪表系数线性度的因素具有非常重要的应用意义。
以上内容来源于网络,如有侵权请联系即删除!



