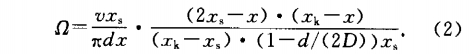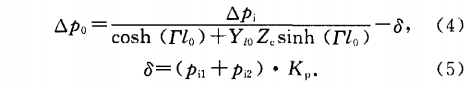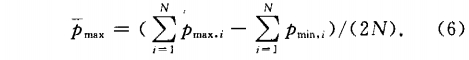摘要:为了提高金宝搏app的抗干扰性和稳定性并保证测量精度,提出了一种基于管壁差压的旋涡频率检测新方法.在水和空气不同管内流动介质的情况下进行了系统实验.应用旋涡动力学和流体阻抗法,分析了取压位置和引压管频率特性因素对该方法测量性能的影响.结果表明,在旋涡发生体下游的一定距离内,取压位置对该方法的斯特劳哈尔数和仪表系数的影响很小,较靠近旋涡发生体迎流面的地方可测流量下限低.引压管的长度应尽量短,并且保证其固有频率与涡街频率相差较大该方法简便可靠,适应性强,测量下限低.
旋涡频率的检测是金宝搏app的关键,压电晶体法是目前最为常用的检测方法.但是压电晶体检测法存在两个严重的问题:1)压电晶体对管道的振动较敏感.2)压电晶体长期使用的稳定性差.为了解决上述问题,研究人员从传感器的结构形式和流量信号的分析处理等方面进行了广泛深人的研究,取得了大量的成果,但是都难以从根本上予以解决.
根据流体力学基本原理,在对金宝搏app流场数值仿真的基础上提出了金宝搏app旋涡频率检测的管壁差压法,并对在不同管径方向的取压位置也作了研究.结果表明,该方法简便可靠,不干扰管道内的流动,抗干扰性强,从而形成一种新型.的金宝搏app,即管壁差压式金宝搏app本文在已有的研究基础上,应用旋涡动力学和流体阻抗法的有关原理,从取压位置和差压检测系统两个方面人手,分析了各种因素对管璧差压式金宝搏app测量的影响,提出了相应的解决方案,为优化测量提供了引导.
1测量原理与特点
在金宝搏app中,有旋涡产生的地方必有压力的变化,交替产生的旋涡必然会导致附近流场的压力出现规则的变化,其变化的频率与旋涡的频率一一对应,因此可以通过检测发生体尾流中某确定的两点间的波动差压来测量旋涡频率,从而实现流量的测量.由于发生体两侧对称点上的相位差为180°,且振动幅度和频率相等,因此将差压取压位置选取在管壁上的对称点更利于检测,如图1所示,其中图1(a)、(b)分别为沿着管道轴向和径向的截面图.
数值仿真结果都表明,与目前常用旋涡频率检测方法相比,管壁差压法具有以下明显优势:1)引压系统对管内待测介质流动几乎没有影响;2)传感器系统独立于旋涡发生体,并且位于管道外面,维修和更换时不需要切断管流拆卸旋涡发生体,可以实现传感器在线维修和更换;3)与压电晶体法相比,具有较强的抗干扰性;4)可测流量下限低.

2过程与装置
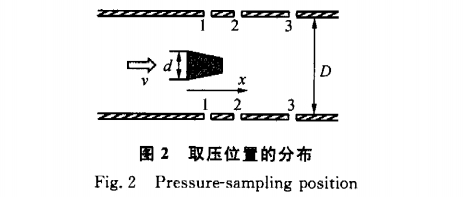
在管内流动介质分别为水和空气的情况下均进行了实验,整个测试由动力设备、稳压设备、标准流量表、前直管段、实验段和后直管段6部分组成.管道的内直径D=50mm,旋涡发生体的横截面为梯形,迎流面宽度d=14mm,管壁差压的取压孔选择在发生体后的三对不同位置1、2、3,它们分别位于距发生体迎流面0.2D、0.5D、D的下游,其中D为管道内直径,如图2所示.
空气和水的标准流量表分别为钟罩标准流量装置和金宝搏app,它们的精度均为0.5级.测得的管壁差压经过放大,由数字示波器记录保存,再导人计算机进行处理分析.
3取压位置的影响
3.1涡街流计内的旋涡特性
由于管壁的约束,金宝搏app中旋涡的产生和脱落特性并不和自由流场中的情况完全相同.金宝搏app中旋涡发生体下游的旋涡区可以分为3个区段,即密集发展段、稳定段和旋涡消散段.在密集发展段,旋涡旋度2(即涡量)沿流动方向x的变化规律为.

式中:v为管内平均流速,D为管道内直径,d为旋涡发生体迎流面宽度,xs为密集发展段的长度.
在稳定段,旋涡旋度为
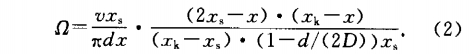
式中:xk为密集发展段和稳定段的总长度.
由于d、D、x,和xk均为常数,根据式(1),(2)可见,不论是在密集发展段还是在稳定段,旋涡旋度Ω都是正比于流速v,且随x的增大而减小.
在旋涡消散段,由于流层之间的相互作用能量逐渐消耗,旋涡逐渐消失.
3.2不同取压位置的实验结果与比较
3.2.1斯特劳哈尔数和仪表系数金宝搏app
用于测量的前提条件是在--定的雷诺数Re范围内仪.表系数K保持为常数,对于金宝搏app,由于K与斯特劳哈尔数St存在如下关系:

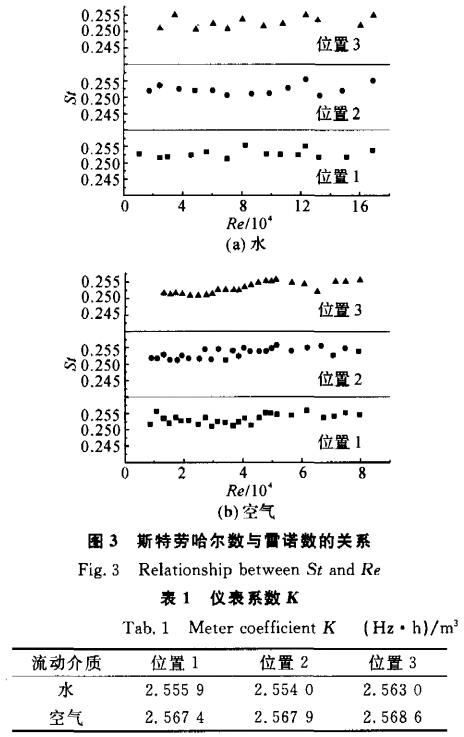
因此要求在一定的雷诺数Re范围内St保持不变.不同流动介质、不同取压位置的St与Re的对应关系如图3(a)、(b)所示.各种情况的St基本上保持为常数,且它们的值均相等,约为0.253.各种情况的仪表系数列于表1,它们之间的最大相对误差小于1%,这表明在旋涡发生体后一定的距离内,流动介质和取压位置对管壁差压式金宝搏app的测量影响很小.
3.2.2最小可测流速
金宝搏app测量下限的拓展一直是研究的热点.各种情况的最小可测流速及常规金宝搏app的测量下限列于表2.在实验中,越靠近发生体,旋涡的旋度强,测量的灵敏度高,不论是水还是空气,最小可测流量都是随取压位置的后移而增大.当测量水时,位置1的测量下限仅为常规表的52%;当测量空气时,位置1的测量下限为常规表的75%,因此采用管壁差压法能有效地降低金宝搏app的测量下限,将取压位置适当靠近发生体能进一步降低测量下限.

引压管的影响
4.1引压管动态特性的数学模型
根据流体阻抗法的集中参数模型,若差压传感器两根引压管的平均长度为Ɩ0,平均导纳为YƖ0,输入的管壁正弦脉动压力差△pi=pil-pi2,则传至差压传感器的差压为
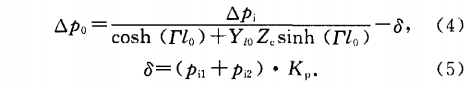
式中:F=√ZY为引压管单位长度的传播常数;Z和Y分别为单位长度的串联阻抗和并联导纳;Zc=√Z/Y为管路的特性阻抗;δ为差压测量的绝对误差;K。为压力脉动影响系数.
在两段引压管长度较短且相差不大,差压传感器压力腔室很小的条件下,当输人差压脉动频率ƒ低于引压管的基本频率ƒ。的1/2时,Kp<0.03,δ值较小;当ƒ>0.5ƒ。时,Kp随ƒ的增.加而显著上升,δ值较大.
4.2管壁差压平均幅值的测最偏差与讨论
管壁差压平均幅值`Pmax定义为
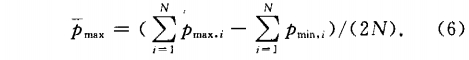
式中:Pmax.pmin,;分别为第i个旋涡周期内管壁差压的最大值和最小值;N为检测的总周期数. `Pmx值反映了旋涡强度的大小,应随流量的增加而增大.实验`Pmx与qv的关系如图4所示,当图4(a)中给出的是流动介质为水时,从3对不同取压位置测量的`Pmx随qv的分布情况,可见3条曲线均随qv的增加而单调递增,较好地符合了理论预测;图4(b)中所示的是流动介质为空气时的情况,3条曲线的形状相似,当qv<83m3/h,`Pmx随流量的增加而增大,在qv=83m3/h附近取得极大值,当qv>83m3/h,`Pmx不再随流量的增加而增大,而是急剧下降直至qv>120m3/h后逐渐平缓递增.
当流量qv=83m3/h时,旋涡频率ƒ=213Hz,K=2.5680Hz·h/m;引压管的长度Ɩ=0.20m,其固有频率ƒ0=c/(4Ɩ)=425Hz,c为引压管中介质的声速,则ƒ=0.5ƒ0..当qv>83m3/h,ƒ>0.5ƒ0,Kp随ƒ的增加而显著上升,差压测量的绝对误差δ值增大.因此较低的引压管固有频率阻碍了测压系统对动态管壁差压的响应,从而造成较大的测量误差,与理论关系不符.为了克服或减小引压管对测量的影响,应尽量缩短引压管的长.度.但是管壁差压幅值的误差并没有影响频率的测量,对St和K的影响甚小,也即流量的测量几乎不会受影响,说明管壁差压法的强适应性和稳定性.

5结论
(1)在发生体下游的一定距离内,取压位置对管壁差压式金宝搏app的斯特劳哈尔数和仪表系数的影响很小;
(2)管壁差压式金宝搏app的测量下限随取压位置的不同而显著变化,在旋涡发生体后的一定范围内,较靠近发生体迎流面的地方测得的最小流速低于远离迎流面的地方;
(3)引压管的响应频率对管壁差压式金宝搏app的测量有着重要的影响,为了保证准确测量,应尽量缩短引压管的长度,并且保证引压管固有频率与涡街频率相差较大.
由于工业现场的流动状态复杂,因此进一步工作将围绕着该方法在旋转流、脉动流等恶劣工况下的性能展开.
本文来源于网络,如有侵权联系即删除!