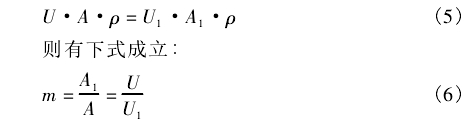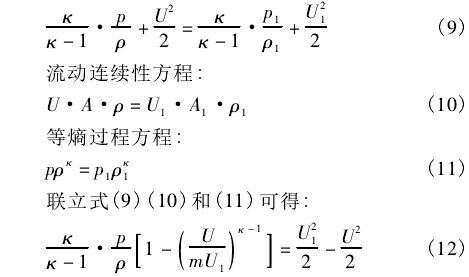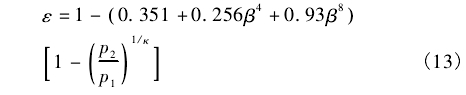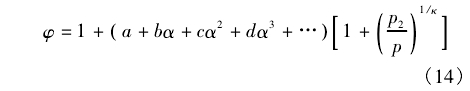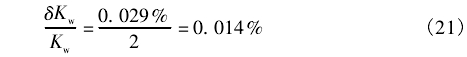摘要:基于金宝搏app基本原理,结合流体力学分析了介质可压缩性对金宝搏app计量特性的影响。考虑到金宝搏app流动截面突然改变导致流体介质参数发生改变的现象与差压式流量计有相似之处,类比标准孔板的介质可膨胀性系数经验公式提出基于介质可压缩性的金宝搏app仪表系数修正数学模型。通过最小二乘拟合对实流标定实验数据进行数值分析得到仪表系数的可压缩性修正公式。最后分析了修正仪表系数的误差和不确定度,最大误差为-0.64%,相对扩展不确定度均在1%以内。研究结果对采用蒸汽介质的金宝搏app仪表系数跨介质标定具有引导意义。
0引言
近年来金宝搏app依靠其结构简单、无可动部件、压损小、量程比宽等优点被广泛应用于液体、气体和蒸汽等介质的流量计量领域中。目前,国内外对于金宝搏app的量值溯源,普遍认为可以进行跨介质标定”在一定雷诺数范围内,金宝搏app旋涡分离频率对被测流体压力、温度、粘度和组分变化不敏感,在几何相似和动力相似条件下可用一种典型介质(水或空气)进行标定。基于这种认识,在对用于蒸汽计量的金宝搏app进行量值溯源时,同时受限于蒸汽实流检测装置运行成本高、安全性等因素,实际工作中通常使用水介质或者空气介质代替蒸汽介质进行实流标定。但由于蒸汽介质具有高温、高压、可压缩等特点,实际工作状态与标定介质空气或水相去甚远。随着金宝搏app在蒸汽计量领域越来越广泛的应用,计量纠纷也不断见诸报道,引起了人们的关注。
对金宝搏app在不同流体介质下的.计量特性以及影响润街流量计计量特性的可能因素进行了大量研究。从謊体力学角度出发,根据相似原理分析了压缩空气代替蒸汽进行蒸汽流量计检定的可能性。对金宝搏app进行了空气和蒸汽实谎标定测试对比分析,结果表明两者标定流量对比误差为2.5%。对介圜温度.介质雷诺数、检定管道内径与金宝搏app测量管径不匹配、魔润发生体尺寸改变等l起金宝搏app仪表系数变化的因素徹了分析。采用数值模报的方法研究了旋润发生体形状对金宝搏app中流动特性的影响,结果表明:聯蔚型发生体下游旋润脱落稳定性更好,且斯特劳暗尔数飯流速(雷诺数)变化较小。国从可压縮流体的流体力学方程出发对金宝搏app的流场进行了分析.将介圆可压缩性对金宝搏app计量.特性的影响日结到流体等鹘指数x,得出介质可压细性会造成仪表系数K值增大.且題介质来流速度的增大这种偏差逐渐增大,文章还通过实流测试和CFD仿真得到润街谎量计在空气和水介圈下的仪表系数偏差,验证了理论分析。从金宝搏app仪表系数K的定义式出发总结出影响金宝搏app计量特性的主要因素为温度和介质可压馏性.为了直观地显示各变量可压细性的影响程度.编辑采用指数报合的方法以压力p密度ρ和等嫡指数x为自变量得到了介质可压缩性影响报合公式考虑到温度对发生体形变的影响,l入材料线性酈胀系数描述温度对仪表系数的影响,最后将这两个因素综合到一起得到系数修正计算方法。苏庆文等国为了研究介圜可压缩性对金宝搏app计量特性的影响,利用FluentApp对金宝搏app在蒸汽、空气和水三种介圜下进行仿真研究,结果表明三种介圆下仪表系数从大到小依次为:空气、蒸汽.水.说明空气受介质的可压细性影响最大.许文达等即对6台不同口径的金宝搏app分别在音速晴嘴法气体流量标准装置和冷凝称重法蒸汽流量标准裝置上进行蒸汽和空气介圜下的实验研究结果显示空气介圈下的仪表系数整体上大于蒸汽介质下的值.
从目前对金宝搏app在不同介圜下的计量特性的相关研究来看,标定介质的可压缩性、温度以及雷诺数,旋涡发生体的几何尺寸等是影响金宝搏app跨介质标定的主要因素,受此影响,采用空气或水介质作为标定介质对蒸汽流量计量金宝搏app进行实流标定会产生一定程度的偏差。为保证蒸汽计量金宝搏app的计量可靠性、节约计量溯源成本、避免蒸汽贸易计量差额,有必要对金宝搏app在蒸汽介质.与空气、水介质下的计量特性进行研究,分析金宝搏app跨介质标定影响因素的作用机理,并做出针对性修正。现有的相关研究中,针对金宝搏app在不同介质下的计量特性的实验研究,测试流量点分布基本按照最大量程的不同百分比来划分(如最大流量点的60%.40%等),这种简单的对应关系没有考.虑介质雷诺数的影响,缺乏理论支撑;一些研究人员从可压缩流体遵循的物理方程出发,分析整理出与介质可压缩性有关的变量,并进行了数值拟合得到介质可压缩性理论拟合公式,这种理论分析计算结果与实流实验数据存在--定偏差,不能完全满足跨介质标定的系数修正的实际需求。
该文从金宝搏app基本原理出发,结合流体力学基本原理,研究介质可压缩性对金宝搏app计量特性的影响,提出基于介质可压缩性的仪表系数修正数学模型,最后对按照雷诺相似准则进行的实流实验数据进行数值分析,通过最小二乘拟合得到仪表系数的可压缩性修正公式。
1金宝搏app基本原理
1.1卡门涡街
金宝搏app依据的基本原理为“卡门涡街”原理。具体来讲,在测量管道中垂直地插入一-段非流.线型阻流体称之为旋涡发生体,来流流体流过发生体,当管道内雷诺数达到--定值时,在发生体下游两侧会交替分离出规则排列的旋涡,这种现象称为卡门涡街现象,如图1所示。在一定雷诺数范围内旋涡脱落频率与发生体两侧的平均流速的关系可表示为中:

式中:ƒ为旋涡脱落频率,Hz;Sr为斯特劳哈尔数;U1为发生体两侧流体平均流速,m/s;d为发生体迎流面的宽度,m。
测量管内的瞬时体积流量qv可表示为:

式中:qv为测量管内瞬时体积流量,m3/s;U为介质来流平均流速,m/s;D为测量管道内径,m。
定义金宝搏app仪表系数K[1/m3]如下:

对于金宝搏app,斯特劳哈尔数Sr在一定管道雷诺数ReD范围内为常数[10]由式(4)可知,金宝搏app几何尺寸一定,在来流速度一定的情况下,在合适的管道雷诺数范围内其仪表系数K仅与发生体两侧的平均流速U1有关,通常用仪表系数K来表征金宝搏app的计量特性。
1.2不可压缩流体
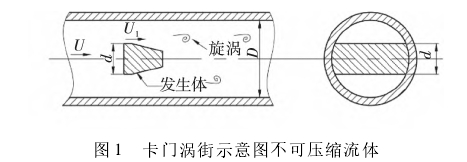
对于不可压缩流体,流体介质在流经发生体前后密度保持不变,根据流体连续性定理可得:
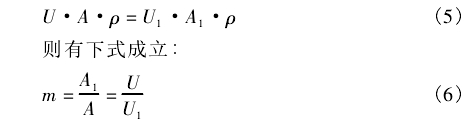
式中:A1为发生体两侧弓形区域面积,m2;A为管道横截面积,m3;ρ为介质来流密度,kg/m3;m为发生体两侧弓形面积与管道横截面积之比。
m的计算式为:

由式(8)可以看出,斯特劳哈尔数Sr--定时,对于不可压缩流体介质,金宝搏app仪表系数K仅与金宝搏app几何尺寸D、d有关,因此,在忽略介质可压缩性影响的情况下,金宝搏app在不同介质下的标定结果具有通用性,这就是金宝搏app跨介质标定的理论依据。
1.3可压缩流体
对于可压缩流体,由于流体介质流经发生体前后密度发生变化,流动过程遵循以下方程:
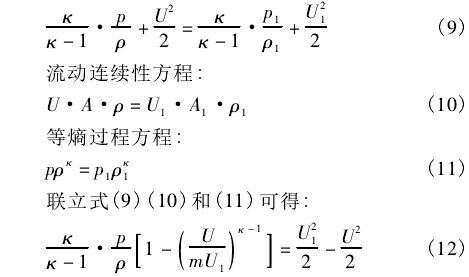
式中:K为流体等熵指数;ρ为发生体两侧介质密度.kg/m3;p为管道横截面处介质压力,Pa;p1为发生体两侧介质压力,Pa。
式(12)描述了可压缩流体介质来流速度U与发生体两侧介质平均流速U1的关系,可以看出两者不仅与金宝搏app几何尺寸有关,还与介质等熵指数、压力、密度有关,且由式(4)己推知,金宝搏app仪表系数K与发生体两侧介质流速成正比。因此,若考虑介质可压缩性的影响,则金宝搏app在不同介质下的通用标定性不再成立,即仪表系数不能简单等同。
2可压缩性修正数学模型
可压缩流体在流经旋涡发生体时,其密度、压力.会发生变化,这种由于流动截面突然改变导致流体介质参数发生改变的现象常见于流量测量和流动控制领域。例如利用流体流经节流件形成局部收缩,从而导致流速增加、压力降低,在节流件前后形成压差的差压式流量计。受此启发,该文参考介质可压缩性对差压式流量计的影响提出针对金宝搏app的可压缩性修正数学模型。
该文选择典型差压式流量计--标准孔板流量计作为参考对象,理由是其发展时间久、理论研究充分。国际标准ISO5167-2:2003中n给出了针对可压缩流体的标准孔板可膨胀性系数经验公式:
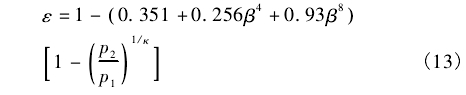
式中:ε为可膨胀性系数;β为节流孔直径与测量管直径的比值;p,为节流孔上游压力,Pa;p2为节流孔下游压力,Pa;K为流体等熵指数。
基于1.3中的理论分析,参考标准孔板的可膨胀性系数经验公式,考虑金宝搏app几何尺寸、压力、等熵指数的影响,提出金宝搏app可压缩性修正因子数学模型如下:
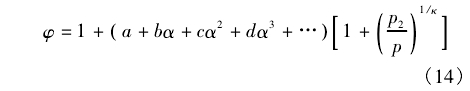
式中:Φ为可压缩性修正因子;a,b,c,d为修正常数;α为金宝搏app几何参数变量;p为介质来流压力,Pa;p2为测量管道下游压力,Pa。
类比标准孔板的等效孔径比β的概念,提出金宝搏app几何参数变量α.其几何意义为金宝搏app有效流通面积与测量管道截面面积之比m的平方根,计算式为:

3数据拟合
为了求得上一节中提出的压缩性修正公式,即解得修正常数a,b,c..,该文对实流标定实验数据进行数值分析,采用离散数据拟合的方法12进行求解。
实验选取水作为不可压缩介质、空气为可压缩介质,以金宝搏app仪表系数K为修正目标提出以下修正公式:

式(17)中等号左侧为关于几何参数变量α的幂函数,a,b,c,d...为待求值,等号右侧带入实验数据后为已知量,则仪表系数K的修正公式问题转化为式(17)表示的线性拟合问题。带入金宝搏app[13]在水和空气介质下的实验数据最终求得修正因子拟合公式如下:

4修正公式误差及不确定度分析
4.1修正误差分析
为验证上述修正因子拟合公式的正确率,进行了误差分析。误差计算公式为:

式中:δ为修正误差,%;K'gas为空气介质仪表系数修正值,1/m3;Kgas为空气介质仪表系数实验值,1/m3。
四台不同口径实验用金宝搏app仪表系数K的修正结果如图2~5所示。
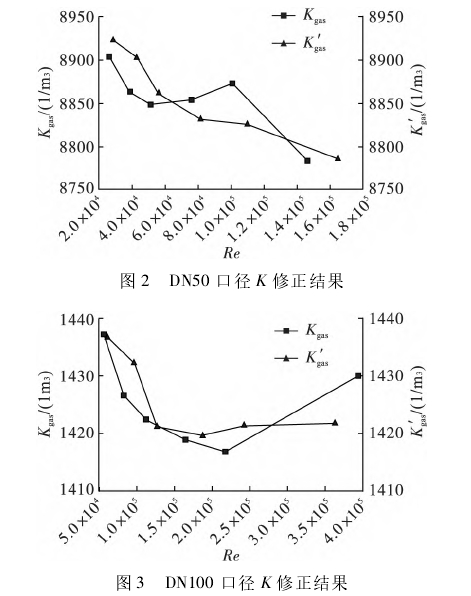
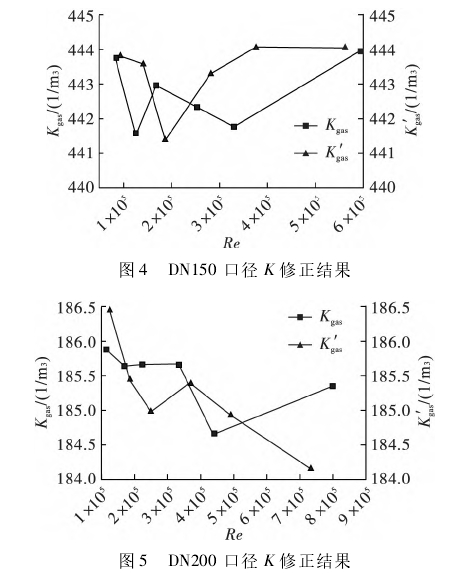
修正误差计算结果如表1所示。

4.2修正公式不确定度分析
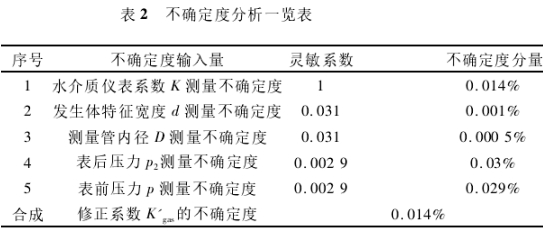
由第三节分析可知修正系数的不确定度输入量包括:水介质仪表系数K的测量不确定度、发生体特征宽度d的测量不确定度、测量管内径D的测量不确定度、压力测量的不确定度等。则修正系数的相对标准不确定度的计算公式如下:

4.2.1水介质仪表系数K
水介质仪表系数K的测量采用静态质量法水3流量标准装置,其流量范围为(0.2~680)rm3/h,测量扩展不确定度为Ur=0.029%,k=2,则:
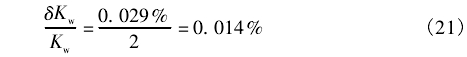
4.2.2发生体特征宽度d和测量管内径D
发生体特征宽度和测量管内径的测量采用激光跟踪仪,查询该装置的校准证书得到其测量不确定.度为:UL=(0.5+0.3L)μm,h=2,则:

以DN50的分析结果为例,将各不确定度分量汇总如表2所示。
4.2.4拟合方法引入的不确定度
考虑曲线拟合法引入的不确定度提出拟合方法的不确定度计算公式如下:

式中:δI为各测试点的修正误差,%;n为测试点个数;v为拟合常数个数(自由度)。
4.2.5合成标准不确定度
综上,修正系数的合成标准不确定度为:

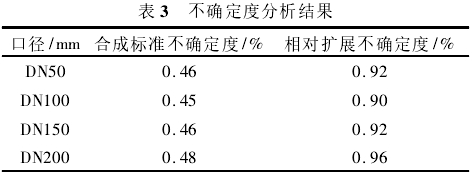
4台不同口径的金宝搏app的不确定度分析结果如表3所示。
5结论
该文针对介质可压缩性对金宝搏app仪表系数的影响,提出了基于介质可压缩性的仪表系数修正数学模型,通过对水和空气介质下的实流实验数据的数值分析,拟合得到仪表系数的可压缩性修正公式,最大误差为-0.64%,相对扩展不确定度均在1%以内。该文的研究方法对于蒸汽介质金宝搏app的仪表系数标定具有引导意义,后续工作可针对水和蒸汽以及空气和蒸汽之间的仪表系数修正开展。
本文来源于网络,如有侵权联系即删除!