摘要:通过研究粘度对浮子流量传感器测量的影响,运用实验手段,测出粘度为10~50mm³/s的.4050航空润滑油对浮子流量传感器的影响误差约为10%左右。结合浮子流量传感器的边界层理论与内部流体流动情况,运用CFDApp仿真,将粘度对DN40mm浮子流量传感器影响误差控制在5%以内。从流场的角度分析浮子流量传感器粘度影响规律及其机理,并且模式化仿真模型,为以后流量传感器的仿真提供了借鉴作用。
浮子流量传感器是以浮子在垂直锥形管中随着流量变化而升降,改变它们之间的流通面积来进行测量的体积流量仪表,又称转子流量传感器或变面积流量传感器”。浮子流量传感器测量精.度受流动介质密度和粘度影响较大。国内外一些学者做了大量试验研究2.3,试图减小这两个方面对测量精度的影响。叶佳敏通过大量粘度实验得到流量与不同浮子高度之间的关系曲线和非牛顿流体的粘度影响规律。
4个粘度共24个流量点的实流实验,然后通过数值仿真求解了两个粘度共12个流量点的流量情况,并根据仿真模型结构化出另外两个粘度12个流量点的仿真模型,与实验对比,仿真误差在5%以内。由此总结出DN40mm锥管浮子流量传感器多粘度仿真模型,该模型便于以后深入研究浮子流量传感器粘度影响机理和优化减粘浮子的结构。
1实验研究
本实验介质为4050航空润滑油,实验粘度范围为10~50mm2/s。采用称重法标定流量传感.器,控制系统采用变频稳压方式,装置精度为5%0。系统根据设定的工作压力和流量值,由变频器控制油泵的输出功率。该装置采用改变介质温度的方式改变介质粘度值,其中有一套完整的加热和冷却系统,实验管道内设置有温度传感器,随时采集实验介质温度,通过温度与介质粘度的对应关系,给出实验介质的粘度值。实验装置如图1所示。
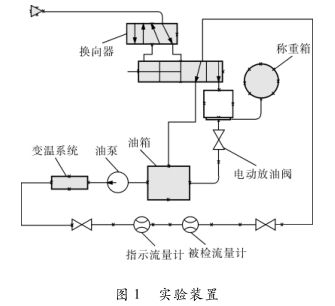
用称重法在可变粘度流量标准装置上检定该流量传感器,检定过程为:调节变频器,使标定软.件测量到的电压值分别对应流量传感器9.0mi、0.2qxomas、0.4qxomas、0.6qxomas、0.8qqxomas和qxomas6个刻度值上,记录标准表流量和介质温度。利用刻度换算公式将表盘上水刻度值换算到实际流体的流量值。
对量程范围1~10m³/h、精度等级1.5级的DN40mm浮子流量传感器进行实验研究。qxo是刻度流量,qvomax为流量传感器量程上限,qv是实际流量,δ1是满度误差,δ1=|(qy0-qy)1/qxomax100%,实验数据见表1。
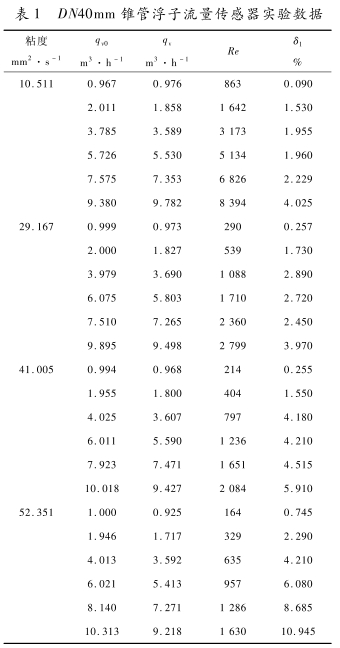
从表1可以看出:
a.
同一粘度流体,满度误差随着流量的增大而增大。根据边界层理论,同一种粘度的流体,当.流量增大时,浮子壁面上边界层的厚度会变薄,而边界层内流速的速度梯度会变大,从而导致浮子.所受的粘性切应力变大,所以流量越大,满度误差.越大。
b.不同粘度的同一种流体,在同一流量下,满度误差随着粘度的增大而增大。根据边界层理.论,不同粘度的流体流过浮子流量传感器时,粘度越大,边界层厚度越大,流体的有效流通面积就越小,另外,粘度的增大导致浮子受到的粘性切应力变大。因此,必须减小浮子流量传感器的入口流.量才能使浮子处在某一高度时,维持受力平衡。
2仿真研究
2.1App概况
计算流体力学(ComputationalFluidDynam-ics,CFD)是利用计算机求解描述流体流动规律的控制方程组技术,涉及到流体力学、计算方法及计算机图形处理等技术。
2.2湍流模型的选择
SSTk-ɷ模型是MenterFR提出的标准k-ɷ模型的一个变形8。该模型合并了来源于ɷ方程中的交叉扩散,并且湍流粘度的计算考虑到了湍流剪应力的传播。该模型可以较好地计算边壁和环隙附近流体的束缚流动情况,还可以正确计算.湍流核心区域流体的流动情况。该模型在近壁自由流中较标准的k-ɷ模型有着更高的精度,在湍流核心区域的计算较标准k-ɷ模型有更广泛的应用。
选择的仿真介质为运动粘度范围10~50mm2/s的航空润滑油,粘性影响明显。粘性流体流经浮子流量传感器时,由于粘性的影响,浮子流量传感器内雷诺数迅速减小,并且考虑到浮子.与导向杆的壁面约束作用,通过比较,选择SSTk-ɷ模型作为浮子流量传感器的湍流模型。
在GAMBIT中做出浮子流量传感器的二维模型,并划分网格,然后把模型导入到FLUENTApp.中,进行湍流模型的设置、人口条件设置、计算模型选择、介质属性设置及浮子表面粗糙度设置等操作。
2.3仿真结果
对10mm²/s和50mm²/s粘度的12个流量点建立模型并进行数值求解,误差在5%以内。针对30mm²/s和40mm²/s粘度的12个点,在FLU-ENT建模时,只移动浮子的位移即可,其他的网格都是模块化的,FLUENT中的设置只有粘度项和人口速度不同,其他完全相同。仿真结果表明:误.差也在5%以内。
2.3.1仿真误差分析
令仿真流量为q,则相对误差δy=1(qf-qv0)I/qy0×100%,不同粘度下流量的相对误差如图2所示。
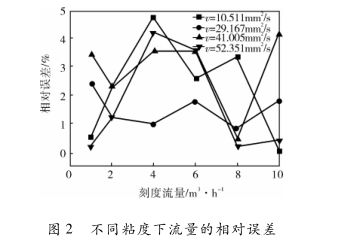
由图2可知,不同粘度下所得的仿真流量和实际流量的误差均未超过5%,说明数值仿真建模、划分网格、选择湍流模型以及求解控制参数等方面都是合理的。CFD数值仿真流场与实验流场吻合,CFD数值仿真模型能够很好地反映实验结.果。
2.3.2速度云图及其分析
为了直观地反映同一流量点不同粘度下流量传感器中速度的变化,选取0.6qyDmax时不同粘度.下X方向速度进行分析,速度云图如图3所示。
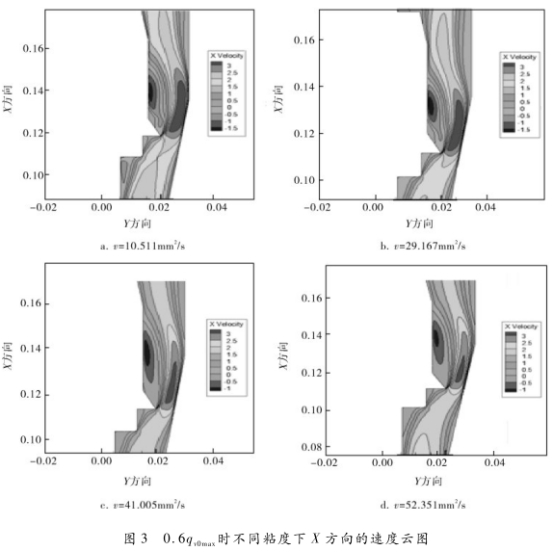
由图3可以分析出:
a.在同一刻度流量点,X方向的速度和速度梯度随着流动介质粘度的增大而减小。原因是流体的粘度增大了,内部摩擦力增大,流体克服摩擦力做功增加,从而压力损失增大,速度和速度梯度都减小了。
b.在同一刻度流量点,随着流体粘度增大,流体通过环隙后的漩涡尾流区影响变小。原因是流体粘度减小,速度明显减小,雷诺数减小,漩涡.的传播速度减小,而同时粘性切应力变大,涡量的衰减速度增大。
2.3.3环隙速度分析
刻度流量为0.6qv0max的仿真模型,其轴向103.5mm处为锥管截面积最大处也就是环隙处,提取了环隙处的速度数值,绘制曲线如图4所示。
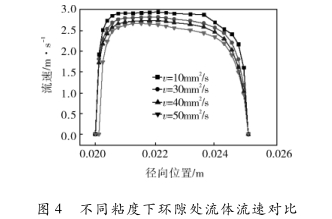
从图4可以看出,环隙处流体的速度随着粘度的增大而减小。原因是同一刻度流量下,环隙的面积是相同的,而流体介质的粘度增大,则其内.部摩擦力消耗增大,使流过环隙处的速度降低。
3数值仿真与实验数据对比
仿真的满度误差小于5%,而实验数据的满度误差是11%,二者不同的主要原因为:
a.实验数据本身存在着误差。该实验是通过改变温度来改变介质粘度的,但是实验过程中温度并非恒定,有一定的波动,所以温度值有一定的误差,从而根据温度取得的密度和粘度值也有误差。
b.仿真的粘度值与实验的粘度值有误差。实验是每个流量点正反行程都测了两次,而仿真的粘度值是取各次实验的平均值,设定参数,每个流量点的粘度只有一个数值。这种方法必然导致流体的仿真粘度和实验粘度存在误差。
C.仿真本身存在误差。流场是连续的,但是CFD数值仿真是采用离散化的手段对流场进行迭代计算。如果网格较少,则计算结果不够正确,会产生误差;如果网格过多,会使截断误差增大,同样也会引起较大误差。
4结束语
通过实验和数值仿真,总结出粘度对浮子流量传感器的影响。通过对比发现,数值仿真可以更透彻地看到管体内部流体的流动情况,但是数值仿真需要经验和对流场状态的基本把握,需要一定的理论基础,而实验可以获得大量新的的资料,可以将数值仿真作为实验的有效补充。
本文来源于网络,如有侵权联系即删除!




